Rohan's blog

Estimating π by throwing needles

Buffon's needle #

Discussion on X

The Buffon's Needle experiment is a cool Monte Carlo method to approximate π! 🪡

gif of simulation of needles and pi value being highlighted

When you throw a needle of length LL onto a piece of ruled paper, it intersects the lines if x<=Lsin(θ)x <= L\sin(\theta), where 𝑥 is the distance from the bottom of the needle to the closest line above it.

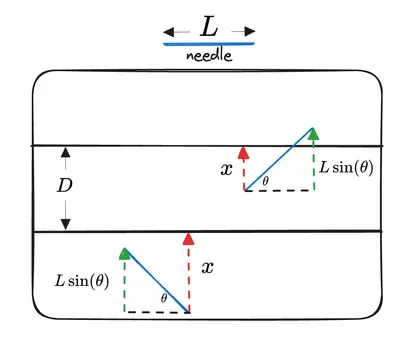
Positions when a needle is thrown onto a piece of paper

Assuming that 𝑥 and 𝜃 are uniformly distributed, for an intersection, we require 0<=θ<=π0<=\theta<=\pi and 0<=x<=Lsin(θ)0<=x<=L\sin(\theta). The probability of this is given by the integral:

P(intersection)=∫0π∫0Lsinθ1Dπdxdθ=2LDπP(\text{intersection}) = \int_{0}^{\pi}\int_{0}^{L\sin\theta}\frac{1}{D\pi}dxd\theta = \frac{2L}{D\pi}

We can estimate the probability of intersection via repeated random trials (needles intersecting line / needles thrown) and rearrange the equation to get a Monte Carlo approximation of π:

π=2LD∗P(intersection)\pi=\frac{2L}{D*P\text({intersection})}

I've made a colab notebook where you can mess around with this simulation in an interactive way. Play with it here! => Interactive simulation